Find the 11th term of the geometric sequence – Embarking on the exploration of geometric sequences, this comprehensive guide delves into the intricacies of finding the 11th term of a geometric sequence. Geometric sequences, characterized by a constant ratio between successive terms, find applications in diverse fields, ranging from finance to biology.
Join us as we unravel the formula, explore real-world applications, and uncover the extensions and variations of geometric sequences.
In this guide, we will delve into the concept of geometric sequences, providing a step-by-step guide to finding the 11th term. Through examples and exercises, we will reinforce understanding and explore the practical applications of geometric sequences.
Understanding Geometric Sequences

A geometric sequence is a sequence of numbers in which each term after the first is found by multiplying the preceding term by a fixed nonzero constant called the common ratio.
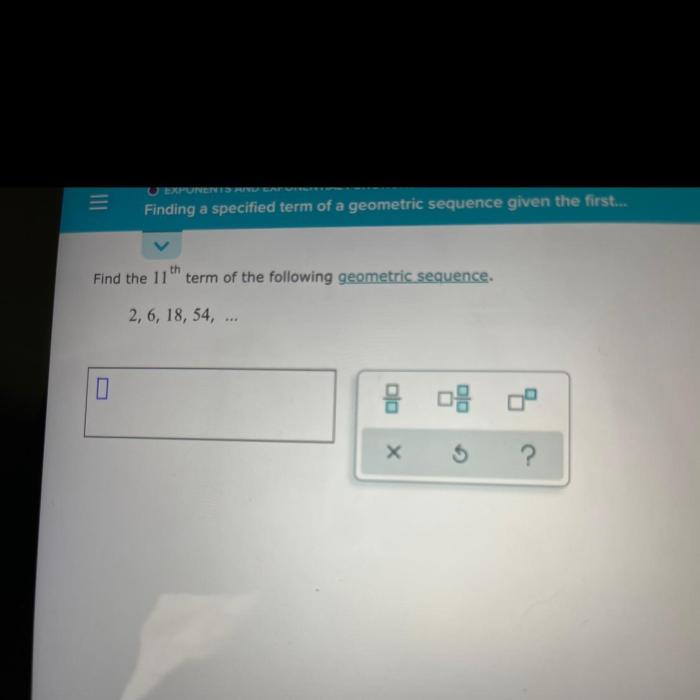
An example of a geometric sequence is 2, 6, 18, 54, 162, … where the common ratio is 3.
The formula for the nth term of a geometric sequence is:
$$a_n = a_1 \cdot r^n-1$$
where:
- $a_n$ is the nth term of the sequence
- $a_1$ is the first term of the sequence
- $r$ is the common ratio
- $n$ is the number of the term
Finding the 11th Term
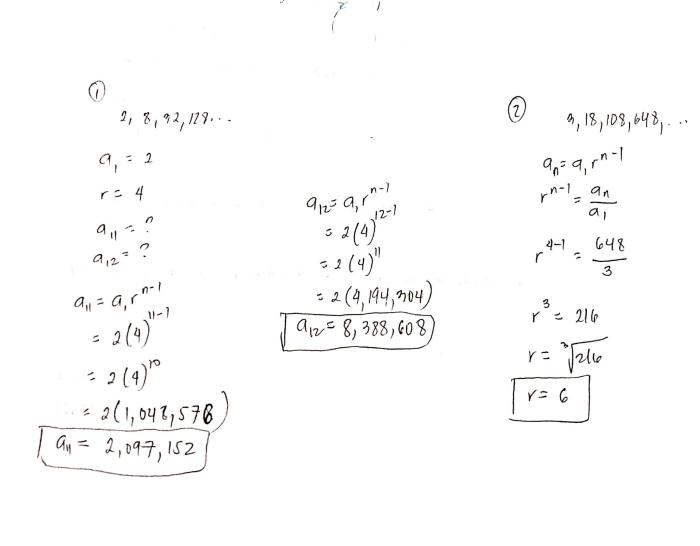
To find the 11th term of a geometric sequence, we use the formula:
$$a_11 = a_1 \cdot r^11-1$$
where:
- $a_11$ is the 11th term of the sequence
- $a_1$ is the first term of the sequence
- $r$ is the common ratio
For example, if we have a geometric sequence with first term $a_1 = 2$ and common ratio $r = 3$, then the 11th term is:
$$a_11 = 2 \cdot 3^11-1 = 2 \cdot 3^10 = 19683$$
Applications of Geometric Sequences
Geometric sequences are used in many real-world applications, such as:
- Finance: Geometric sequences are used to calculate compound interest and present value.
- Biology: Geometric sequences are used to model population growth and decay.
- Physics: Geometric sequences are used to model the decay of radioactive isotopes.
For example, if we have a bank account with an interest rate of 5% per year, then the amount of money in the account after n years is given by the geometric sequence:
$$a_n = P \cdot (1 + 0.05)^n$$
where:
- $a_n$ is the amount of money in the account after n years
- $P$ is the initial amount of money in the account
- $r$ is the interest rate
- $n$ is the number of years
Extensions and Variations
Geometric sequences have several variations, such as:
- Infinite geometric series: An infinite geometric series is a geometric sequence that has an infinite number of terms.
- Geometric means: The geometric mean of two numbers is the nth root of their product.
Geometric sequences are also used in other fields, such as:
- Finance: Geometric sequences are used to calculate the present value of an annuity.
- Biology: Geometric sequences are used to model the growth of bacteria.
- Computer science: Geometric sequences are used to analyze the running time of algorithms.
Key Questions Answered: Find The 11th Term Of The Geometric Sequence
What is a geometric sequence?
A geometric sequence is a sequence of numbers where each term after the first is found by multiplying the previous term by a constant called the common ratio.
How do I find the 11th term of a geometric sequence?
To find the 11th term of a geometric sequence, use the formula: a11 = a1 – r^10, where a1 is the first term and r is the common ratio.
What are some real-world applications of geometric sequences?
Geometric sequences are used in various fields, including finance (compound interest), biology (population growth), and physics (radioactive decay).